Division
Equal Sharing
What is Division as Equal Sharing?
Division as equal sharing means dividing something into equal parts or groups. The goal is to find out how many items each group will get if you share them equally.
Example: Sharing Cookies
Let’s say you have 12 cookies, and you want to share them equally among 4 friends. How many cookies will each friend get?
1. Start with the Total Number:
– You have 12 cookies.
2. Decide on the Number of Groups:
– You want to share the cookies with 4 friends, so you need to divide the cookies into 4 equal groups.
3. Share the Cookies Equally:
– Start by giving each friend 1 cookie until you run out of cookies.
– Give 1 cookie to the first friend, then 1 to the second friend, and so on until all cookies are given out.
4. Count the Cookies in Each Group:
– After you’ve shared all the cookies, count how many each friend has.
– Each friend gets 3 cookies.
So, if you divide 12 cookies among 4 friends, each friend gets 3 cookies. In math, this is written as:
12 ÷ 4 = 3
Important Points :
– Equal Sharing: Division is all about making sure each group gets the same amount. No group should have more or fewer items than the others.
– Understanding Division: Explain that division is like the opposite of multiplication. Instead of putting groups together, you’re breaking them apart equally.
– Real-Life Examples: Use everyday situations (sharing snacks, dividing toys) to help them understand the concept.
Practice Problems:
1. If you have 10 apples and want to share them with 5 friends, how many apples does each friend get?
– 10 ÷5 = 2
2. If you have 15 pencils and want to share them with 3 classmates, how many pencils does each classmate get?
– 15 ÷ 3 = 5
Equal grouping
Division as equal grouping is a concept where you divide a total number into groups of a specific size and then count how many groups you can make.
What is Division as Equal Grouping?
Division as equal grouping means taking a certain number of items and putting them into groups of the same size, then figuring out how many groups you have.
Example: Grouping Toys
Let’s say you have 12 toys, and you want to make groups of 3 toys each. How many groups can you make?
1. Start with the Total Number:
– You have 12 toys.
2. Decide on the Size of Each Group:
– You want each group to have 3 toys.
3. Make Groups:
– Start grouping the toys by putting 3 toys together at a time.
– Keep making groups until you run out of toys.
4. Count the Number of Groups:
– After you’ve grouped all the toys, count how many groups you have.
– You should have 4 groups.
So, if you divide 12 toys into groups of 3, you can make 4 groups. In math, this is written as:
12 ÷ 3 = 4
Important Points :
– Equal Grouping: Division is about making sure all groups have the same number of items. Each group should have the same size.
– Understanding Division: Explain that division is about finding out how many groups you can make with a specific number of items in each group.
Practice Problems:
1. If you have 15 marbles and want to put them into groups of 5, how many groups can you make?
– 15 ÷ 5 = 3
2. If you have 20 stickers and want to group them into sets of 4, how many groups can you make?
– 20 ÷ 4 = 5
Difference Between Equal Sharing and Equal Grouping:
– Equal Sharing: You know the number of groups and want to find out how many items each group gets.
– Equal Grouping: You know how many items each group should have and want to find out how many groups you can make.
Division as repeated subtraction
What Is Division?
Division is when we want to see how many times one number can fit into another number.
Division as Repeated Subtraction
You can think of division as repeatedly subtracting the same number from a bigger number until you can’t subtract anymore. The number of times you subtract is the answer to the division problem!
Example: 12 ÷ 3
Let’s divide 12 by 3.
1. Start with 12.
2. Subtract 3: 12 – 3 = 9.
3. Subtract 3 again: 9 – 3 = 6.
4. Subtract 3 again: 6 – 3 = 3.
5. Subtract 3 one more time: 3 – 3 = 0.
You subtracted 3 four times until you got to 0. So, 12 ÷ 3 = 4.
Another Example: 15 ÷ 5
Let’s divide 15 by 5.
1. Start with 15.
2. Subtract 5: 15 – 5 = 10.
3. Subtract 5 again: 10 – 5 = 5.
4. Subtract 5 one more time: 5 – 5 = 0.
You subtracted 5 three times until you got to 0. So, 15 ÷ 5 = 3.
Why It Works
Division as repeated subtraction works because you’re simply finding out how many times you can take a certain number away from the original number until there’s nothing left. This tells you how many groups of that number fit into the original number.
Division on number line
What Is Division?
Division is when we want to find out how many times one number can fit into another number. It’s like sharing or grouping things equally.
Using a Number Line to Understand Division
A number line is a straight line with numbers marked at equal distances. We can use this line to show division by making jumps backward from the bigger number to 0, using the smaller number.
Steps to Show Division on a Number Line
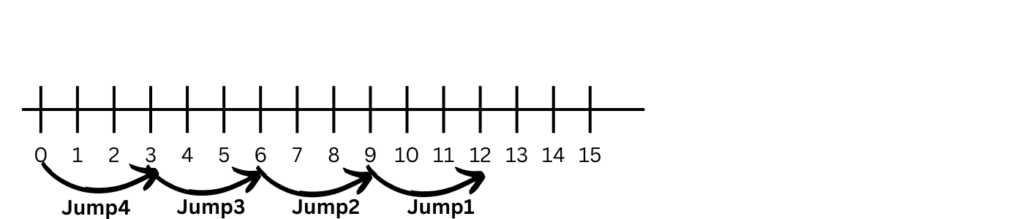
Let’s use the example 12 ÷ 3 to show how division works on a number line.
Step 1: Draw a Number Line
– Draw a straight line and mark numbers on it, starting from 0. Make sure you include all numbers up to the larger number in your division problem. In this case, you’ll mark from 0 to 12.
#### Step 2: Start at the Larger Number
– Place your finger or a marker at the larger number (12 in this case) on the number line.
Step 3: Make Equal Jumps Backward
– From 12, you will make equal jumps backward by the smaller number (which is 3). Each jump is like subtracting 3 from your starting number.
– Jump 1: From 12 to 9 (subtract 3).
– Jump 2: From 9 to 6 (subtract 3).
– Jump 3: From 6 to 3 (subtract 3).
– Jump 4: From 3 to 0 (subtract 3).
Step 4: Count the Jumps
– Count how many jumps you made to get from 12 to 0. In this case, you made 4 jumps.
Step 5: Write the Answer
– The number of jumps is the answer to the division problem. So, 12 ÷ 3 = 4.
Here’s what it looks like:
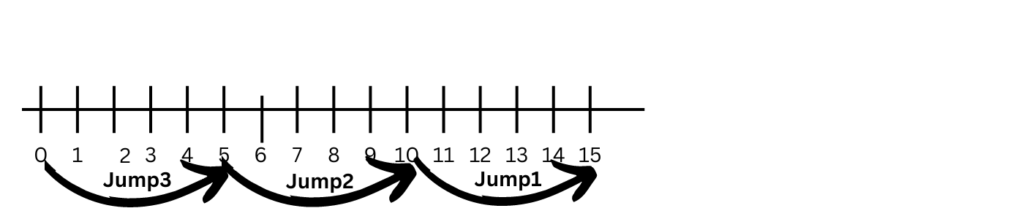
Another Example: 15 ÷ 5 on a Number Line
1. Draw the Number Line: Mark it from 0 to 15.
2. Start at 15: Place your finger at 15.
3. Make Jumps of 5:
– Jump 1: From 15 to 10.
– Jump 2: From 10 to 5.
– Jump 3: From 5 to 0.
4. Count the Jumps: You made 3 jumps.
5. Write the Answer: So, 15 ÷ 5 = 3.
Relation between multiplication and division
What Is Multiplication?
– Multiplication is like adding the same number over and over again.
– For example, if you have 3 groups of 4 apples, you can multiply 3 × 4 to find out how many apples there are in total. (3 × 4 = 12).
What Is Division?
– Division is about sharing or splitting a number into equal groups.
– For example, if you have 12 apples and you want to share them equally among 3 friends, you can divide 12 ÷ 3 to find out how many apples each friend gets. (12 ÷ 3 = 4).
How Are Multiplication and Division Related?
1. Opposite (Inverse) Operations:
– Multiplication and division are like opposites. If you know one, you can figure out the other.
– Example: If you know that 4 × 3 = 12, then you also know that 12 ÷ 4 = 3 and 12 ÷ 3 = 4.
2. Multiplication to Understand Division:
– If you know a multiplication fact, you can use it to understand division.
– Example: If you know 5 × 2 = 10, you can understand that 10 ÷ 2 = 5 and 10 ÷ 5 = 2.
Example to Show the Relationship:
Imagine you have 4 baskets, and each basket has 3 oranges:
– Multiplication: To find out the total number of oranges, you multiply 4 baskets by 3 oranges in each basket (4 × 3 = 12 oranges).
– Division: If you know there are 12 oranges and you want to put them into 4 equal baskets, you divide 12 oranges by 4 baskets (12 ÷ 4 = 3 oranges in each basket).
Simple Fact Family:
A fact family shows how multiplication and division are connected using the same numbers.
– For the numbers 2, 3, and 6:
– Multiplication: 2 × 3 = 6 and 3 × 2 = 6.
– Division: 6 ÷ 2 = 3 and 6 ÷ 3 = 2.
Division using multiplication tables
Division is like splitting something into equal parts. It’s also like finding out how many times a number fits into another number.
Using Multiplication Tables:
We can use multiplication tables to help understand division. Let’s see how.
Example 1: Dividing 12 by 3
– Step 1: Think of division as asking, “How many 3s fit into 12?”
– Step 2: Look at the multiplication table of 3:
– 3 × 1 = 3
– 3 × 2 = 6
– 3 × 3 = 9
– 3 × 4 = 12
– Step 3: We see that 3 multiplied by 4 gives 12. This means 12 divided by 3 equals 4.
So, 12 ÷ 3 = 4.
Example 2: Dividing 15 by 5
– Step 1: Think of division as asking, “How many 5s fit into 15?”
– Step 2: Look at the multiplication table of 5:
– 5 × 1 = 5
– 5 × 2 = 10
– 5 × 3 = 15
– Step 3: We see that 5 multiplied by 3 gives 15. This means 15 divided by 5 equals 3.
So, 15 ÷ 5 = 3.
Practice:
– Use different numbers and look at their multiplication tables to find out how division works. For example:
– 16 ÷ 4: Look at the table of 4 and see that 4 × 4 = 16, so 16 ÷ 4 = 4.
– 20 ÷ 5: Look at the table of 5 and see that 5 × 4 = 20, so 20 ÷ 5 = 4.
Key Points :
1. Division is about sharing equally or finding out how many times one number fits into another.
2. Multiplication and division are related: If you know one, you can figure out the other.
3. Practice with tables: Use multiplication tables to help with division questions.
Terms related to division
When learning about division, there are a few important words that can help you understand how division works.
1. Division
– What It Is: Division is when you split something into equal parts or groups. It’s like sharing candy with friends and making sure everyone gets the same amount.
– Symbol: The symbol for division is `÷`.
2. Dividend
– What It Is: The dividend is the big number you want to divide. It’s the total amount that you want to split up.
– Example: If you have 12 candies and want to share them with friends, 12 is the dividend.
3. Divisor
– What It Is: The divisor is the number you divide by. It’s how many groups or people you are dividing the dividend into.
– Example: If you’re sharing the 12 candies with 3 friends, 3 is the divisor.
4. Quotient
– What It Is: The quotient is the answer you get when you divide the dividend by the divisor. It’s how many candies each friend will get.
– Example: If you divide 12 candies among 3 friends, each friend gets 4 candies. So, the quotient is 4.
5. Remainder
– What It Is: Sometimes when you divide, there might be some left over that can’t be evenly divided. This leftover part is called the remainder.
– Example: If you have 10 candies and share them with 3 friends, each friend gets 3 candies, and 1 candy is left over. The remainder is 1.
Example of Division Using These Terms:
Let’s say you want to divide 20 chocolates among 4 friends.
– Dividend: 20 (the total chocolates)
– Divisor: 4 (the number of friends)
– Quotient: 5 (each friend gets 5 chocolates)
– Remainder: 0 (there’s nothing left over, so the remainder is 0)
Putting It All Together:
– 20 ÷ 4 = 5
– Dividend ÷ Divisor = Quotient
– There is no remainder in this case.
Key Points :
1. Division means splitting things into equal parts.
2. The dividend is the total amount.
3. The divisor is the number of parts or groups.
4. The quotient is the result, or how many each part gets.
5. The remainder is what’s left over if the division isn’t exact.
Understanding the properties of division helps us see how division works and why it’s different from addition, subtraction, and multiplication.
1. Division by 1
– What It Means: When you divide any number by 1, the number stays the same.
– Example: If you have 10 apples and divide them among 1 person, that person gets all 10 apples.
– 10 ÷ 1 = 10
2. Division by the Same Number
– What It Means: When you divide a number by itself (the same number), the answer is always 1.
– Example: If you have 5 candies and give all 5 to 1 friend, your friend gets 1 whole group of candies.
– 5 ÷ 5 = 1
3. Division of 0 by Any Number
– What It Means: When you divide 0 by any number, the answer is always 0.
– Example: If you have 0 chocolates and try to share them with 3 friends, each friend gets 0 chocolates.
– 0 ÷ 3 = 0
4. Division by Zero (Not Possible)
– What It Means: You cannot divide a number by 0. It’s like trying to share something with nobody—it doesn’t make sense.
– Example: If you have 10 candies, you can’t divide them by 0 because there’s no one to share them with.
– 10 ÷ 0 = Not possible
Key Points :
1. Dividing by 1 keeps the number the same.
2. Dividing a number by itself always gives 1.
3. Dividing 0 by any number gives 0.
4. You cannot divide a number by 0.
Long division method
Long division is a way to divide big numbers into smaller parts, step by step. It might seem tricky at first, but with practice, it becomes easier. Let’s go through the steps to help you understand how it works.
Steps for Long Division
Let’s divide 84 by 4 using long division.
1. Set Up the Problem
– Write 84 (the number you want to divide) under a long division bracket.
– Write 4 (the number you’re dividing by) outside the bracket.
____
4 | 84
2. Divide
– Start with the first digit of the dividend (the number inside the bracket). Look at 8.
– Ask: “How many times does 4 go into 8 without going over?”
– 4 goes into 8 two times. Write 2 above the bracket.
2__
4 | 84
3. Multiply
– Multiply the divisor (4) by the number you just wrote above (2).
– 4 × 2 = 8.
– Write 8 under the 8 in 84.
2__
4 | 84
-8
4. Subtract
– Subtract 8 from 8.
– The answer is 0.
– Write 0 below.
2__
4 | 84
-8
0
5. Bring Down the Next Digit
– Bring down the next digit in the dividend, which is 4.
– Now, you have 4.
2__
4 | 84
-8
04
6. Repeat the Process
– Now, ask: “How many times does 4 go into 4?”
– 4 goes into 4 one time. Write 1 above the bracket next to the 2.
21_
4 | 84
-8
04
7. Multiply Again
– Multiply the divisor (4) by the number you just wrote (1).
– 4 × 1 = 4.
– Write 4 under the 4 you just brought down.
21_
4 | 84
-8
04
-4
8. Subtract Again
– Subtract 4 from 4.
– The answer is 0.
– There’s nothing left to bring down, so you’re done!
21
4 | 84
-8
04
-4
0
Final Answer
– The quotient is 21.
– 84 ÷ 4 = 21.
Key Points :
1. Divide the first number.
2. Multiply the divisor by the number above the bracket.
3. Subtract to find the remainder.
4. Bring down the next digit and repeat until you’ve brought down all digits.
Division with remainder
Division with remainder happens when you divide a number and there’s something left over that can’t be evenly divided. Let’s break it down with simple examples and steps.
Understanding the Terms
– Dividend: The number you want to divide.
– Divisor: The number you are dividing by.
– Quotient: The result of the division.
– Remainder: What’s left over if the division isn’t exact.
Example: Dividing 13 by 4
1. Set Up the Problem
– You want to divide 13 (the dividend) by 4 (the divisor).
– Write it like this: 13 ÷ 4.
2. Divide
– Ask: “How many times does 4 fit into 13 without going over?”
– 4 fits into 13 3 times because 4 × 3 = 12.
3. Multiply
– Multiply 4 (the divisor) by 3 (the number of times it fits).
– 4 × 3 = 12.
– Write 12 under the 13.
4. Subtract
– Subtract 12 from 13.
– 13 – 12 = 1.
– Write 1 as the remainder.
Result
– 13 ÷ 4 = 3 with a remainder of 1.
Practice Examples
1. 22 ÷ 5
– 5 goes into 22 4 times because 5 × 4 = 20.
– Subtract 20 from 22 to get a remainder of 2.
– 22 ÷ 5 = 4 , remainder-2
Key Points :
1. Divide the number as much as you can.
2. Multiply to find out how many times the divisor fits into the dividend.
3. Subtract to see what’s left.
4. The leftover part is the remainder.
