Divison (1-20)
Division is a mathematical operation where we split a number into equal parts. Let’s explain division with an example up to 20 for a class 1 student:
Let’s take the division problem: 10 ÷ 2
Here, 10 is the total number we want to divide, and 2 is the number of equal groups we want to divide it into.
To solve this:
– We start with 10 items (let’s say 10 apples).
– We want to divide these 10 apples into 2 equal groups.
So, we give 5 apples to each group:
Group 1: 5 apples
Group 2: 5 apples
Each group now has 5 apples. Therefore, 10 ÷ 2 = 5.
Let’s do another one: 15 ÷ 3
Here, 15 is the total number we want to divide, and 3 is the number of equal groups we want to divide it into.
To solve this:
– We start with 15 items (for example, 15 cookies).
– We want to divide these 15 cookies into 3 equal groups.
So, we give 5 cookies to each group:
Group 1: 5 cookies
Group 2: 5 cookies
Group 3: 5 cookies
Each group now has 5 cookies. Therefore, 15 ÷ 3 = 5.
In division, we also use a division symbol (÷) and a division sentence like:
10 ÷ 2 = 5
Regrouping
Understanding Regrouping in Division
Division is splitting a number into equal parts. Regrouping in division means rearranging groups to divide more efficiently, especially when the divisor is larger than some of the digits in the dividend.
Steps to Teach Regrouping in Division
1. Introduce Division Vocabulary:
– Dividend: The number to be divided.
– Divisor: The number by which the dividend is divided.
– Quotient: The result of the division.
2. Start with Simple Division:
– Use objects like counters, blocks, or drawings to show division.
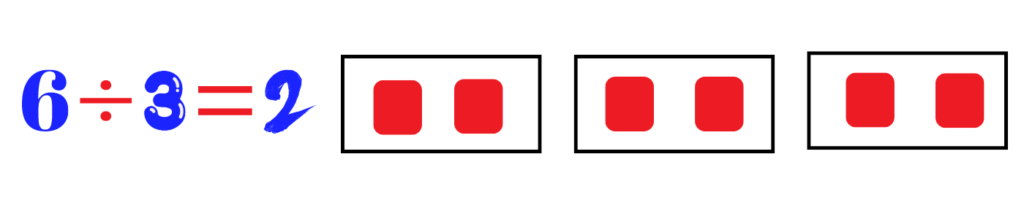
– Example: 6 ÷ 2
– Divide 6 blocks into 2 equal groups.
– Each group has 3 blocks, so 6 ÷ 2 = 3.
3. Explain Regrouping Concept:
– Regrouping is used when you can’t divide a digit in the dividend directly by the divisor.
– Example: 15 ÷ 3
– Show 15 blocks.
– Try to make 3 equal groups.

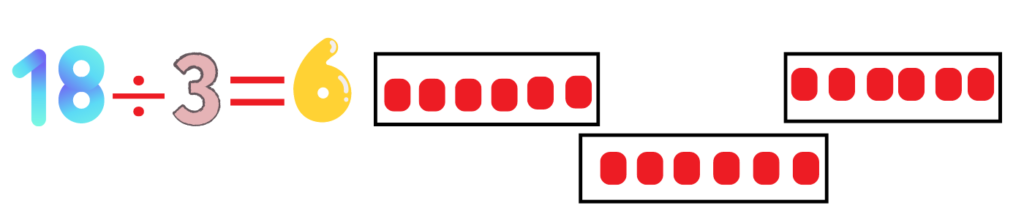
4 . Example: 18 ÷ 3
– Write the problem on the board.
– Draw 18 objects (like circles).
– Group the objects into sets of 3.
– Count how many sets of 3 you have. (You’ll have 6 sets).
– So, 18 ÷ 3 = 6.
Division as repeated subtraction
Division as repeated subtraction is a simple concept that helps us understand how division works by thinking of it as repeatedly taking away groups of equal size. Here’s an explanation:
Imagine you have 12 candies and you want to share them equally among 3 friends. Division helps us find out how many candies each friend will get.
1. Repeated Subtraction Method:
– Start with the total number of candies, which is 12.
– You want to share these candies equally among 3 friends.
– Think of division as taking away (subtracting) equal groups (or parts) from the total.
Let’s do it step by step:
– Start with 12 candies.
– Give 3 candies to each friend, one at a time.
– 12 candies – 3 candies = 9 candies left.
– 9 candies – 3 candies = 6 candies left.
– 6 candies – 3 candies = 3 candies left.
– 3 candies – 3 candies = 0 candies left.
So, you can see that by subtracting 3 candies each time (because you have 3 friends), you find out that each friend gets 4 candies (because you subtracted 3 candies 4 times).
Therefore, 12 candies divided by 3 friends equals 4 candies per friend.
