Division
Long division method
Let’s divide 43,265 ÷ 21.
Step 1: Set up the division
Write 43,265 (the dividend) inside the division bracket and 21 (the divisor) outside the bracket.
Step 2: Divide the first part
Look at the first two digits of 43,265, which is 43.
Now, see how many times 21 fits into 43. It fits 2 times, because 21 × 2 = 42 (which is close to 43 but not bigger than it).
– Write 2 above the line, over the digit 3 in 43,265.
– Multiply 2 × 21 = 42 and write it below 43.
– Subtract 43 – 42 = 1.
Step 3: Bring down the next digit
Now, bring down the next digit, which is 2 (from 43,265). You now have 12.
Step 4: Divide again
Now, divide 12 ÷ 21. Since 12 is smaller than 21, 21 doesn’t fit into 12. So, we write 0 above the line.
– Now, bring down the next digit, which is 6. You now have 126.
Step 5: Continue dividing
Now, divide 126 ÷ 21. It fits 6 times because 21 × 6 = 126.
– Write 6 above the line.
– Multiply 6 × 21 = 126 and subtract 126 – 126 = 0.
Step 6: Bring down the next digit
Bring down the last digit, which is 5. Now you have 5.
Step 7: Divide the last digit
Divide 5 ÷ 21. 21 doesn’t fit into 5, so we write 0 above the line.
So, the answer to 43,265 ÷ 21 is 2,060 with a remainder of 5.

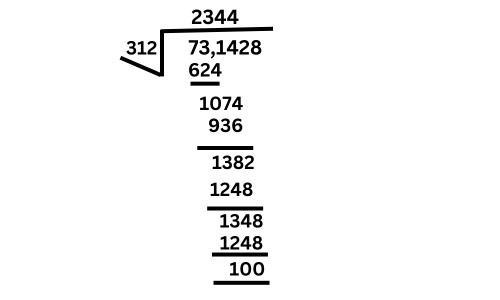
Now, let’s divide 731,428 ÷ 312
Step 1: Set up the division
Write 731,428 (the dividend) inside the division bracket and 312 (the divisor) outside the bracket.
Step 2: Divide the first part
Look at the first three digits of 731,428, which is 731.
Now, divide 731 ÷ 312. It fits 2 times because 312 × 2 = 624.
– Write 2 above the line.
– Multiply 2 × 312 = 624 and write it below 731.
– Subtract 731 – 624 = 107.
Step 3: Bring down the next digit
Bring down the next digit, which is 4 (from 731,428). Now, you have 1,074.
Step 4: Divide again
Now, divide 1,074 ÷ 312. It fits 3 times because 312 × 3 = 936.
– Write 3 above the line.
– Multiply 3 × 312 = 936 and subtract 1,074 – 936 = 138.
Step 5: Bring down the next digit
Bring down the next digit, which is 2. Now, you have 1,382.
Step 6: Continue dividing
Now, divide 1,382 ÷ 312. It fits 4 times because 312 × 4 = 1,248.
– Write 4 above the line.
– Multiply 4 × 312 = 1,248 and subtract 1,382 – 1,248 = 134.
Step 7: Bring down the last digit
Bring down the last digit, which is 8. Now you have 1,348.
Step 8: Divide the last part
Divide 1,348 ÷ 312. It fits 4 times because 312 × 4 = 1,248.
– Write 4 above the line.
– Multiply 4 × 312 = 1,248 and subtract 1,348 – 1,248 = 100.
So, the answer to 731,428 ÷ 312 is 2,344 with a remainder of 100.
Short division method
The short division method is a quick way to divide large numbers without writing down every step in detail.
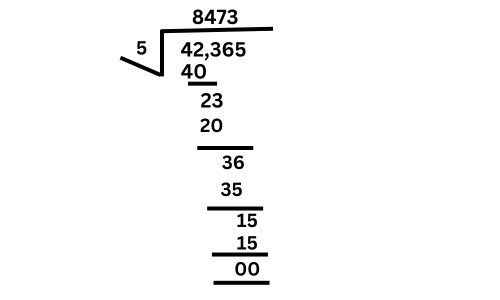
Example 1: Divide 42,365 by 5.
Steps:
1. Divide the first digit (4) by 5:
– 4 ÷ 5 = 0 (since 4 is smaller than 5, it can’t be divided fully)
– Write 0 in the quotient and carry over the 4 to the next digit.
2. Now take the next two digits together (42):
– 42 ÷ 5 = 8 remainder 2.
– Write 8 in the quotient, and carry the remainder (2) to the next digit (which makes it 23 now).
3. Now divide the next number (23) by 5:
– 23 ÷ 5 = 4 remainder 3.
– Write 4 in the quotient, and carry the remainder (3) to the next digit (which makes it 36 now).
4. Next, divide 36 by 5:
– 36 ÷ 5 = 7 remainder 1.
– Write 7 in the quotient, and carry the remainder (1) to the next digit (which makes it 15 now).
5. Finally, divide 15 by 5:
– 15 ÷ 5 = 3.
– Write 3 in the quotient with no remainder left.
Final Answer:
The quotient is 8473.
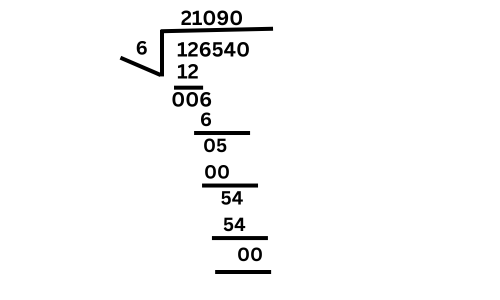
Example 2: Divide 126,540 by 6.
Steps:
1. Divide the first digit (1) by 6:
– 1 ÷ 6 = 0 (since 1 is smaller than 6).
– Write 0 in the quotient and carry over the 1 to the next digit.
2. Now take the next two digits together (12):
– 12 ÷ 6 = 2.
– Write 2 in the quotient, with no remainder.
3. Divide the next digit (6) by 6:
– 6 ÷ 6 = 1.
– Write 1 in the quotient.
4. Next, divide the next digit (5) by 6:
– 5 ÷ 6 = 0 remainder 5.
– Write 0 in the quotient, and carry the remainder (5) to the next digit (which makes it 54 now).
5. Now divide 54 by 6:
– 54 ÷ 6 = 9.
– Write 9 in the quotient.
6. Finally, divide the last digit (0) by 6:
– 0 ÷ 6 = 0.
– Write 0 in the quotient.
Final Answer:
The quotient is 21090.
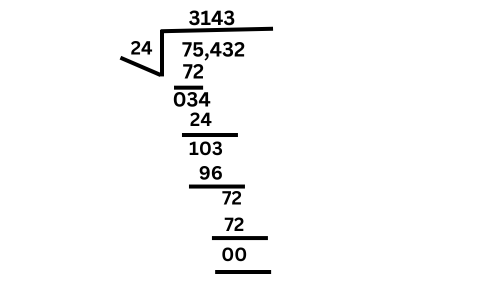
Division by 2-digit numbers
Example 1: Divide 75,432 by 24
Steps:
1. Set up the problem:
– Write 75,432 (dividend) inside the division box and 24 (divisor) outside the box.
2. Look at the first two digits of the dividend (75):
– Ask, “How many times does 24 fit into 75?”
– 24 × 3 = 72. (So, 24 goes into 75 three times.)
– Write 3 above the division bar.
3. Multiply and subtract:
– Multiply 24 × 3 = 72.
– Subtract 75 – 72 = 3.
4. Bring down the next digit (4):
– Bring down the 4 from the next digit of the dividend, making it 34.
5. Divide the new number (34) by 24:
– Ask, “How many times does 24 fit into 34?”
– 24 × 1 = 24.
– Write 1 above the division bar next to the 3.
6. Multiply and subtract:
– Multiply 24 × 1 = 24.
– Subtract 34 – 24 = 10.
7. Bring down the next digit (3):
– Bring down the next digit from the dividend, which is 3, making the new number 103.
8. Divide 103 by 24:
– 24 × 4 = 96 (since 24 fits into 103 four times).
– Write 4 above the division bar next to the 1.
9. Multiply and subtract:
– Multiply 24 × 4 = 96.
– Subtract 103 – 96 = 7.
10. Bring down the last digit (2):
– Bring down the final digit, making the number 72.
11. Divide 72 by 24:
– 24 × 3 = 72.
– Write 3 above the division bar next to the 4.
12. Multiply and subtract:
– Multiply 24 × 3 = 72.
– Subtract 72 – 72 = 0.
Final Answer: The quotient is 3,143.
Example 2:Divide 456,789 by 53
Steps:
1. Look at the first three digits (456):
– Ask, “How many times does 53 fit into 456?”
– 53 × 8 = 424. (53 fits into 456 eight times.)
– Write 8 above the division bar.
2. Multiply and subtract:
– Multiply 53 × 8 = 424.
– Subtract 456 – 424 = 32.
3. Bring down the next digit (7):
– Bring down the 7 from the dividend, making the number 327.
4. Divide 327 by 53:
– 53 × 6 = 318 (53 fits into 327 six times).
– Write 6 above the division bar next to the 8.
5. Multiply and subtract:
– Multiply 53 × 6 = 318.
– Subtract 327 – 318 = 9.
6. Bring down the next digit (8):
– Bring down the 8, making the number 98.
7. Divide 98 by 53:
– 53 × 1 = 53 (53 fits into 98 one time).
– Write 1 above the division bar next to the 6.
8. Multiply and subtract:
– Multiply 53 × 1 = 53.
– Subtract 98 – 53 = 45.
9. Bring down the last digit (9):
– Bring down the final digit, making the number 459.
10. Divide 459 by 53:
– 53 × 8 = 424 (53 fits into 459 eight times).
– Write 8 above the division bar next to the 1.
11. Multiply and subtract:
– Multiply 53 × 8 = 424.
– Subtract 459 – 424 = 35.
Final Answer: The quotient is 8,618 with a remainder of 35.

Division of a number by 10, 100 and 1000
When you divide a number by 10, 100, or 1000, you’re essentially reducing its size by moving the digits to the right.
Division by 10
– When you divide a number by 10, the digits move one place to the right, and the number becomes ten times smaller.
– Example:
250 ÷ 10 = 25
Here, we remove one zero (or move the digits one place to the right), so 250 becomes 25.
Division by 100
– When you divide a number by 100, the digits move two places to the right, and the number becomes one hundred times smaller.
– Example:
6000 ÷ 100 = 60
Here, we remove two zeros (or move the digits two places to the right), so 6000 becomes 60.
Division by 1000
– When you divide a number by 1000, the digits move three places to the right, and the number becomes one thousand times smaller.
– Example:
45000 ÷ 1000 = 45
Here, we remove three zeros (or move the digits three places to the right), so 45000 becomes 45.
What Happens with Decimal Points?
– When there are fewer digits, you’ll need to add a decimal point.
Example:
7 ÷ 10 = 0.7
85 ÷ 100 = 0.85
94 ÷ 1000 = 0.094
In each case, the number gets smaller as the decimal point moves to the left.
Summary:
– Dividing by 10: Move digits 1 place to the right.
– Dividing by 100: Move digits 2 places to the right.
– Dividing by 1000: Move digits 3 places to the right.
Estimating the quotient
Estimating the quotient is a approximate the result of division problems without needing to do the exact calculation.
Steps for Estimating the Quotient:
1. Round the Numbers: Look at the dividend (the number being divided) and the divisor (the number you are dividing by). Round them to numbers that are easier to work with. Typically, you round to the nearest ten or hundred.
Example:
– For 342 ÷ 6, you can round 342 to 340 (or even 300 if you want to make it simpler).
– 6 stays the same since it’s already easy to divide by.
2. Divide the Rounded Numbers: After rounding the numbers, divide them as you normally would. The result will be an estimate of the quotient.
Continuing the example:
– 340 ÷ 6 = approximately 56.7 (or 300 ÷ 6 = 50 if you rounded further).
3. Check if the Estimate is Reasonable: Compare the estimated quotient with the original numbers to make sure it makes sense. The goal is to get a close but quick answer.
Example Problems:
1. Problem: 123 ÷ 4
– Round 123 to 120 (because it’s close to 123).
– 120 ÷ 4 = 30.
– So, the estimated quotient is 30.
2. Problem: 567 ÷ 8
– Round 567 to 560.
– 560 ÷ 8 = 70.
– So, the estimated quotient is 70.
Word Problems :
1. Problem: Distributing Toys
A factory produced 32,000 toy cars, and they want to pack them into boxes with 500 toy cars in each box. How many boxes are needed?
– Solution:
32,000 ÷ 500 = 64
So, they will need 64 boxes.
2. Problem: Sharing Money
A charity raised 125,000 dollars and plans to distribute the money equally among 250 families. How much money will each family receive?
– Solution:
125,000 ÷ 250 = 500
Each family will receive 500.
3. Problem: Distributing Books
A publishing company printed 84,000 books and wants to send them equally to 400 schools. How many books will each school get?
– Solution:
84,000 ÷ 400 = 210
Each school will get 210 book.
