Geometery
Points
A point is a small dot that shows an exact position or location in space.
– Points have no size (no length, width, or height). They are just a mark or a dot.
– We usually label points with capital letters like A, B, C, etc.
Example:
– Draw a point on a paper and label it “A”.
– Now, draw another point and label it “B”.
– The points A and B show two different locations on your paper.

Point A
Point A and point B
Line
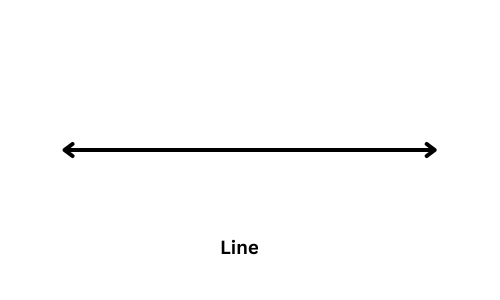
What is a Line?
– A line is a straight path that goes on forever in both directions.
– It has no end points; it never stops.
– A line is usually drawn with arrows at both ends to show that it keeps going.
– We name lines with two points on the line (like points A and B), and we write it as Line AB.
Key Features of a Line:
– Straight: A line is always straight, never curved.
– Infinite: It has no starting or ending point, meaning it keeps extending forever.
Line segment
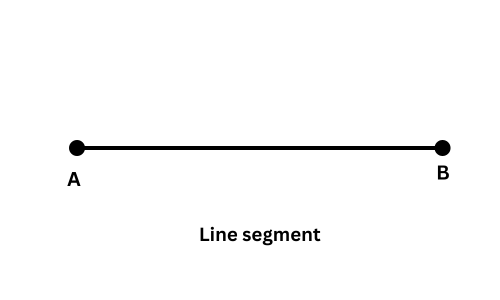
What is a Line Segment?
– A line segment is a part of a line that has two endpoints.
– Unlike a line, a line segment does not go on forever. It has a fixed length because it starts at one point and ends at another.
– We can measure the length of a line segment.
Naming a Line Segment:
– We use the names of the two endpoints to name the line segment. For example, if the two endpoints are A and B, we call it Line Segment AB.
Key Features:
– Straight: Like a line, a line segment is always straight.
– Fixed Length: It has a start and an end, so we can measure how long it is.
Measuring of line segment
What is a line segment?
– A line segment is a part of a line that has two endpoints. It doesn’t go on forever like a line; it stops at the endpoints.
2. What tool do we use to measure a line segment?
– We use a ruler to measure the length of a line segment. Rulers usually have numbers on them to show length in centimeters (cm) or inches (in).
3. How do you measure a line segment?
– Place the ruler so that the 0 mark is exactly at one end of the line segment.
– Look at the number on the ruler that matches the other end of the line segment. That number is the length of the line segment.
4. Units of measurement:
– The length of a line segment is usually measured in centimeters (cm) for short distances. If the segment is longer, you might use meters (m).
5. Example:
– If a line segment starts at 0 cm and ends at 5 cm on a ruler, its length is 5 cm.
Drawing line segment
1. What is a line segment?
– A line segment is a straight path between two points. It has a starting point and an ending point.
2. What do you need to draw a line segment?
– A ruler and a pencil.
3. Steps to draw a line segment:
Step 1: Mark two points
– Place your pencil on the paper and mark a starting point. This is where your line segment will begin.
– Then, move your pencil and mark an ending point where your line segment will stop. You can choose any distance between these points.
Step 2: Use the ruler
– Place the ruler on the paper so that it lines up with the two points you marked. Make sure the ruler is straight.
Step 3: Draw the line segment
– Hold the ruler in place and use your pencil to draw a straight line between the two points.
4. Label the line segment
– After drawing the line, you can label the two points as A and B, so your line segment can be called AB.
5. Practice Example:
– Draw a line segment that is 5 cm long:
– Mark the first point as A.
– Place the ruler so that the 0 cm mark is on point A.
– Mark a second point at the 5 cm mark and label it B.
– Draw a line connecting A and B.
Plane figures
A plane figure is a flat, two-dimensional (2D) shape that lies entirely on a single plane. Here are some common plane figures-
1. Square
– All four sides are of equal length.
– All four angles are right angles (90 degrees).
2. Rectangle
– Opposite sides are of equal length.
– All four angles are right angles (90 degrees).
3. Triangle
– A shape with three sides and three angles.
– There are different types of triangles based on the length of their sides or their angles:
– Equilateral triangle: All sides are equal.
– Isosceles triangle: Two sides are equal.
– Scalene triangle: No sides are equal.
4. Circle
– A round shape where all points on the edge are the same distance from the center.
5. Pentagon
– A shape with five sides and five angles.
6. Hexagon
– A shape with six sides and six angles.
7. Oval
– A shape that looks like a stretched circle.
Properties of Plane Figures:
– Sides: The straight lines that form the boundary of a figure.
– Vertices: The corners where two sides meet.
– Angles: The space between two intersecting sides, usually measured in degrees.
Solid figures
Solid figures are three-dimensional (3D) shapes that have length, width, and height. Unlike plane figures, they take up space and have volume. Here are some common solid figures :
1. Cube
– A cube has 6 square faces, all of the same size.
– It has 12 edges and 8 vertices (corners).
– Example: A dice.
2. Cuboid
– A cuboid has 6 rectangular faces.
– It has 12 edges and 8 vertices.
– Example: A brick or a book.
3. Sphere
– A sphere is perfectly round, like a ball.
– It has no edges or vertices, just one curved surface.
– Example: A basketball or a globe.
4. Cylinder
– A cylinder has two circular faces (top and bottom) and one curved surface in the middle.
– It has no vertices and 2 edges (where the circular faces meet the curved surface).
– Example: A can or a battery.
5. Cone
– A cone has one circular face and one curved surface.
– It has one vertex (the pointy tip) and one edge (around the circular base).
– Example: An ice cream cone or a party hat.
6. Pyramid
– A pyramid has a flat base and triangular faces that meet at a single vertex (tip).
– The base can be a square (square pyramid) or any other polygon.
– Example: The Egyptian pyramids or a tent.
Properties of Solid Figures:
– Faces: Flat or curved surfaces that make up the boundary of a solid figure.
– Edges: The line segments where two faces meet.
– Vertices: The points where the edges meet (corners).
Faces , edges and corners.
Here’s an explanation of faces, edges, and corners (also called vertices) for class 3:
1. Faces
– Definition: Faces are the flat or curved surfaces of a solid figure.
– Example:
– A cube has 6 faces, all of which are squares.
– A cylinder has 3 faces: 2 flat circular faces (top and bottom) and 1 curved face (the side).
2. Edges
– Definition: Edges are the straight lines where two faces of a solid figure meet.
– Example:
– A cuboid has 12 edges where its rectangular faces meet.
– A cone has 1 edge where its circular base meets the curved surface.
3. Corners (Vertices)
– Definition: Corners (or vertices) are the points where edges meet. In 3D shapes, this is where three or more edges come together.
– Example:
– A cube has 8 vertices (corners).
– A sphere has 0 vertices because it has no edges or corners.
Examples of Counting Faces, Edges, and Corners:
– Cube:
– Faces: 6 (square faces)
– Edges: 12
– Corners (Vertices): 8
– Cylinder:
– Faces: 3 (2 flat circular faces and 1 curved face)
– Edges: 2
– Corners (Vertices): 0
– Pyramid:
– Faces: Depends on the base (a square pyramid has 5 faces: 4 triangular and 1 square)
– Edges: Depends on the base (a square pyramid has 8 edges)
– Corners (Vertices): Depends on the base (a square pyramid has 5 vertices)
