Geometery
Point
What is a Point?
– A point is like a tiny dot that shows a place or position.
– It has no size, no length, and no width. It’s just a mark showing “where” something is.
– A point is usually named with a capital letter like A, B, or C.
Example:
Imagine you are drawing a map. If you want to show where your school is, you might draw a small dot. That dot is like a point on the map.
How Points are Used:
– Points help us show locations in geometry.
– We use points to create lines and shapes by connecting them.
Important:
– A point doesn’t have any size—it just shows where something is!
– When drawing a point, we make a small dot and name it with a letter, like Point A.
In short, a point is a small mark that tells us “where” something is in geometry!
Line
What is a Line?
– A line is a straight path that goes on and on in both directions. It never ends.
– It has no thickness, only length.
– You can name a line by using any two points on it. For example, if a line passes through points A and B, we call it Line AB.
Key Features of a Line:
1. Straight: A line is always straight and never curves.
2. Endless: A line keeps going forever in both directions (we use arrows to show this on both ends).
3. Made of Points: A line is made up of many tiny points close together.
Drawing a Line:
– To draw a line, use a ruler to make a straight line on the paper.
– Add small arrows on both ends to show that it doesn’t stop.
– Name the line with two points, like A and B.
Types of Lines:
1. Horizontal Line: A line that goes left to right.
2. Vertical Line: A line that goes up and down.
3. Slanting Line: A line that goes diagonally.
Line Segment
What is a Line Segment?
– A line segment is a straight path that connects two points.
– It has a starting point and an ending point, so it doesn’t go on forever like a line.
– You can name a line segment by its two endpoints. For example, if it starts at point A and ends at point B, it is called Line Segment AB.
Key Features of a Line Segment:
1. Straight: A line segment is always straight.
2. Has Two Endpoints: It starts at one point and ends at another. It does not go on forever.
3. Fixed Length: Because it has two endpoints, a line segment has a specific length that can be measured.
Example:
Think of a pencil. The pencil has a tip at one end and an eraser at the other. The straight part between them is like a line segment—it has two endpoints and a fixed length.
Drawing a Line Segment:
– Use a ruler to draw a straight line on paper.
– Mark two points at the ends and label them with capital letters, like A and B.
– This is Line Segment AB.
How a Line Segment is Different from a Line:
– A line goes on forever in both directions.
– A line segment has two endpoints and stops there. It has a measurable length.
Ray
What is a Ray?
– A ray is a straight path that starts at one point and goes on forever in one direction.
– It has one starting point (called the endpoint) but no ending point.
– You name a ray using its endpoint and one other point on the ray. For example, if it starts at point A and passes through point B, it’s called Ray AB.
Key Features of a Ray:
1. Straight: A ray is always straight.
2. One Endpoint: It starts at one point (the endpoint).
3. Goes Forever in One Direction: A ray keeps going endlessly in one direction. We use an arrow to show that it doesn’t stop.
Drawing a Ray:
– To draw a ray, first make a point (the endpoint), for example, A.
– Then, use a ruler to draw a straight line going from that point and add an arrow at the end to show it keeps going.
– Label another point on the ray, like B, and name it Ray AB.
How a Ray is Different from a Line and a Line Segment:
– A line goes on forever in both directions.
– A line segment has two endpoints and a fixed length.
– A ray has one endpoint and goes on forever in one direction.
Plane
What is a Plane?
– A plane is a flat surface that goes on and on in all directions. It has no thickness, only length and width.
– A plane is like a big sheet of paper, but it keeps extending forever, even though we can only see a small part of it.
– A plane is made up of many points and lines.
Key Features of a Plane:
1. Flat Surface: A plane is perfectly flat, like a tabletop.
2. Endless in All Directions: Even though we might only see a small part of it, a plane extends infinitely in all directions.
3. No Thickness: A plane is flat and has no thickness, only length and width.
Example:
Imagine a blackboard or a piece of paper. These are like small parts of a plane. A plane is like a large, flat surface that extends forever in all directions.
Drawing a Plane:
– We usually draw part of a plane as a four-sided shape (like a rectangle) to represent a small section of it.
– A plane is often named with a capital letter like Plane P or using three points on the plane, such as Plane ABC.
Angle
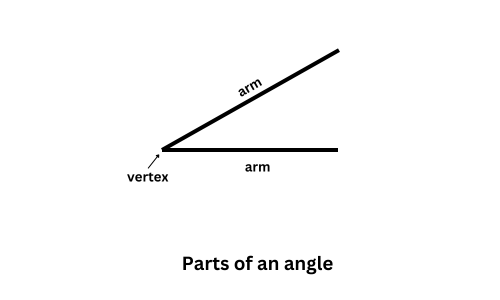
1. Angle: An angle is formed when two lines meet at a point. This point is called the vertex of the angle, and the lines are called the arms of the angle.
2. Parts of an Angle:
– Vertex: The point where the two lines meet.
– Arms: The lines that form the angle.
3. Measuring Angles:
– Angles are measured in degrees (°).
– We use a tool called a protractor to measure angles.
4. Types of Angles:
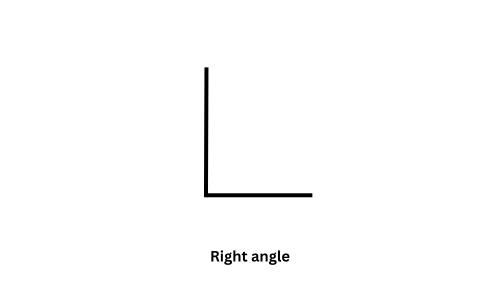
– Right Angle: An angle that is exactly 90°.
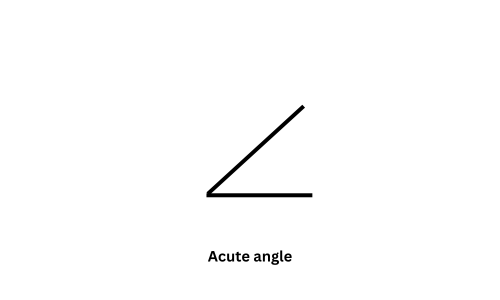
– Acute Angle: An angle that is less than 90°.
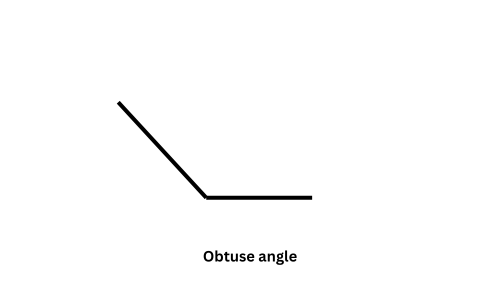
– Obtuse Angle: An angle that is more than 90° but less than 180°.
– Straight Angle: An angle that is exactly 180°.
5. Examples of Angles:
– A right angle can be seen at the corner of a square or rectangle.
– An acute angle looks smaller, like the hands of a clock at 10:00.
– An obtuse angle is larger, like the hands of a clock at 2:00.
Polygon and its types
A polygon is a flat, closed shape made up of straight lines. These lines are called sides. Polygons can have 3 or more sides, and they must be closed, meaning all the sides must connect together.
For example, a triangle is a polygon because it has three straight sides that connect to form a closed shape.
Types of Polygons
Polygons are named based on the number of sides they have. Here are some common types:
1. Triangle:
– A polygon with 3 sides.
– Example: a pizza slice.
2. Quadrilateral:
– A polygon with 4 sides.
– Examples: squares and rectangles.
3. Pentagon:
– A polygon with 5 sides.
– Example: a starfish’s body.
4. Hexagon:
– A polygon with 6 sides.
– Example: a honeycomb cell.
5. Octagon:
– A polygon with 8 sides.
– Example: a stop sign.
Types Based on Sides and Angles
– Regular Polygon: All sides and angles are equal. Example: a square (all sides are the same length).
– Irregular Polygon: Sides and angles can be different. Example: a rectangle (opposite sides are equal, but not all sides are the same length).
Circle and its parts
A circle is a round shape where every point on the circle is the same distance from the center. Unlike polygons, a circle does not have sides or corners. It is perfectly smooth and continuous.
Parts of a Circle
1. Center:
– The exact middle point of the circle. Every point on the circle is the same distance from the center.
– Example: The middle of a pizza.
2. Radius:
– The distance from the center to any point on the circle.
– It’s like drawing a line from the center to the edge of the circle.
– Example: Imagine drawing a line from the middle of a pizza to the edge. That’s the radius.
3. Diameter:
– A line that passes through the center and touches two points on the circle. The diameter is twice as long as the radius.
– Example: If you cut a pizza in half, the line you cut along is the diameter.
4. Circumference:
– The distance around the circle, like the perimeter of a polygon.
– Example: If you walk all the way around a circular park, the distance you walk is the circumference.
5. Chord:
– A line that connects two points on the circle, but does not pass through the center.
– Example: Think of drawing a line between two points on the edge of the pizza without going through the middle.
6. Arc:
– A part of the circle’s edge (circumference). It’s like a curved line between two points on the circle.
– Example: A slice of pizza is part of the circle’s arc.
