Numbers up to 100
Tens and Ones
Each digit in a number has a place value. For numbers up to 100, we focus on the tens place and the ones place.
Place Value:
Ones Place: This is the rightmost digit. It tells us how many ones are in the number.
Tens Place: This is the second digit from the right. It tells us how many groups of ten are in the number.
Let’s break down some examples:
Examples:
1. Number: 23
– Tens Place: 2
– Ones Place: 3
– Explanation: There are 2 groups of ten and 3 ones. This is 20 + 3 = 23.
2. Number: 47
– Tens Place: 4
– Ones Place: 7
– Explanation: There are 4 groups of ten and 7 ones. This is 40 + 7 = 47.
3. Number: 89
– Tens Place: 8
– Ones Place: 9
– Explanation: There are 8 groups of ten and 9 ones. This is 80 + 9 = 89.
4. Number: 56
– Tens Place: 5
– Ones Place: 6
– Explanation: There are 5 groups of ten and 6 ones. This is 50 + 6 = 56.
5. Number: 100
– Tens Place: 10
– Ones Place: 0
– Explanation: There are 10 groups of ten and 0 ones. This is 100 + 0 = 100.
How to Find Tens and Ones:
1. Identify the Tens Place:
– Look at the second digit from the right.
– This digit tells you how many groups of ten are in the number.
2. Identify the Ones Place:
– Look at the rightmost digit.
– This digit tells you how many ones are in the number.
Summary:
– Tens Place tells us the number of groups of ten.
– Ones Place tells us the number of ones.
– Together, they form numbers from 1 to 100.
Understanding tens and ones helps us to see how numbers are built and to do simple math operations like addition and subtraction more easily.
Counting on the Abacus
An abacus is a simple tool used for counting and basic arithmetic. It consists of a frame with rods, each rod having beads that can be moved up and down. The position of the beads on these rods represents different values.
Structure of the Abacus:
– Frame: Holds the rods and beads.
– Rods: Vertical lines within the frame, each representing a place value (ones, tens, hundreds, etc.).
– Beads: Small objects that slide up and down the rods.
In a simple abacus for teaching young children, we often use:
– 1 rod for Ones
– 1 rod for Tens
– 1 rod for Hundreds (if needed)
Using the Abacus to Count:
Step-by-Step Example: Counting to 23
1. Start with an empty abacus: All beads are at the top of the frame, not counted yet.
2. Counting Ones:
– Look at the rod representing the ones place.
– Move one bead down for each number you want to count.
– For the number 3, move three beads down on the ones rod.
3. Counting Tens:
– Look at the rod representing the tens place.
– Each bead on this rod represents ten.
– For the number 20, move two beads down on the tens rod.
4. Combining Tens and Ones:
– You now have two beads down on the tens rod (representing 20).
– You have three beads down on the ones rod (representing 3).
– Together, this shows the number 23.
Visual Representation:
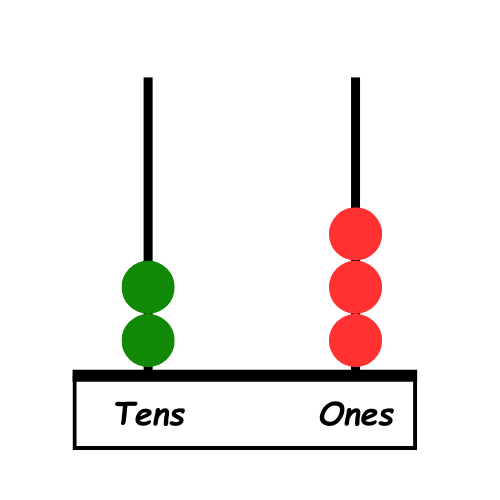
Practice Examples:
1. Number: 15
– Tens Rod: 1 bead down (10)
– Ones Rod: 5 beads down (5)
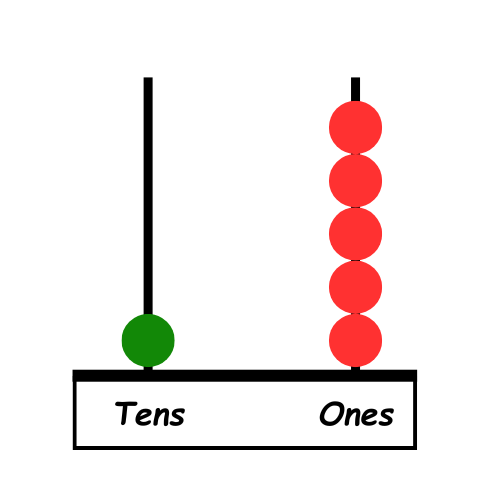
2. Number: 47
– Tens Rod: 4 bead down (40)
– Ones Rod: 7 beads down (7)
Summary:
– Tens Rod: Each bead represents 10.
– Ones Rod: Each bead represents 1.
– Counting: Move beads down to represent the numbers.
By using an abacus, first-grade students can visually and physically count, helping them understand place value and basic arithmetic concepts. This hands-on approach makes learning numbers fun and interactive.
Increasing & Decreasing order
Increasing Order
Increasing order means arranging numbers from the smallest to the largest. Think of it as climbing up a staircase, where each step is a higher number than the one before it.
Example:
Let’s arrange the numbers 5, 2, 9, and 1 in increasing order.
1. Start with the smallest number: 1
2. The next smallest number: 2
3. Then comes: 5
4. Finally, the largest number: 9
So, in increasing order, the numbers are **1, 2, 5, 9**.
Decreasing Order
Decreasing order means arranging numbers from the largest to the smallest. Think of it as going down a slide, where each number is smaller than the one before it.
Example:
Let’s arrange the numbers 8, 3, 7, and 10 in decreasing order.
1. Start with the largest number: 10
2. The next largest number: 8
3. Then comes: 7
4. Finally, the smallest number: 3
So, in decreasing order, the numbers are **10, 8, 7, 3**.
Let’s Try More Examples!
Example of Increasing Order:
Arrange 12, 4, 19, and 7 in increasing order.
1. The smallest number is 4
2. Next is 7
3. Then comes 12
4. The largest number is 19
So, the increasing order is 4, 7, 12, 19.
Example of Decreasing Order:
Arrange 14, 5, 9, and 20 in decreasing order.
1. The largest number is 20
2. Next is 14
3. Then comes 9
4. The smallest number is 5
So, the decreasing order is 20, 14, 9, 5.
Skip Counting
Skip counting means counting forward or backward by a number other than 1. It’s like jumping over some numbers to land on others. Skip counting helps us count faster and can be a lot of fun!
Skip Counting by 2s
When we skip count by 2s, we start at a number and then add 2 each time.
– Start at 0: 0
– Add 2: 2
– Add another 2: 4
– Keep adding 2: 6, 8, 10, 12, 14, 16, 18, 20
So, if we skip count by 2s, the numbers are 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
Skip Counting by 5s
When we skip count by 5s, we start at a number and then add 5 each time.
– Start at 0: 0
– Add 5: 5
– Add another 5: 10
– Keep adding 5: 15, 20, 25, 30, 35, 40, 45, 50
So, if we skip count by 5s, the numbers are 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50.
Skip Counting by 10s
When we skip count by 10s, we start at a number and then add 10 each time.
– Start at 0: 0
– Add 10: 10
– Add another 10: 20
– Keep adding 10: 30, 40, 50, 60, 70, 80, 90, 100
So, if we skip count by 10s, the numbers are 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Ordinal numbers
Ordinal numbers tell us the position or order of something in a list. They show the rank or sequence of items. For example, 1st, 2nd, and 3rd are ordinal numbers.
Examples of Ordinal Numbers
First (1st), Second (2nd), Third (3rd)
Imagine you are in a race with your friends. The order in which you finish the race is described using ordinal numbers.
1. First (1st): The person who finishes the race first is in the 1st position.
2. Second (2nd): The person who finishes the race second is in the 2nd position.
3. Third (3rd): The person who finishes the race third is in the 3rd position.
So, if Amy finishes the race first, Ben finishes second, and Chloe finishes third, we say:
– Amy is 1st.
– Ben is 2nd.
– Chloe is 3rd.
More Examples
Lining Up in a Classroom
Let’s say you and your classmates are lining up to go outside. The order in which you stand in line can be described with ordinal numbers.
1. The person at the front of the line is 1st.
2. The next person is 2nd.
3. The person after that is 3rd.
4. And so on…
Days of the Week
We can use ordinal numbers to describe the days of the week.
1. Monday is the 1st day of the week.
2. Tuesday is the 2nd day of the week.
3. Wednesday is the 3rd day of the week.
4. Thursday is the 4th day of the week.
5. Friday is the 5th day of the week.
6. Saturday is the 6th day of the week.
7. Sunday is the 7th day of the week.
