Number upto 10000
Numbers up to 10,000 have four digits: Thousands, Hundreds, Tens, and Ones. Each digit’s place value shows its worth, like 4,325, where 4 is 4,000, 3 is 300, 2 is 20, and 5 is 5. We read this as “four thousand three hundred twenty-five.” Use place value to expand numbers (e.g., 6,482 = 6,000 + 400 + 80 + 2). Compare numbers by looking at the largest place value first. You can also round numbers to the nearest 10, 100, or 1,000 for easier calculations. Understanding place value helps in reading, writing, and working with large numbers.
4- digit number on abacus
An abacus is a great tool to help understand four-digit numbers visually and hands-on. Here’s how you can explain four-digit numbers using an abacus:
1. Understanding the Abacus Structure
– An abacus typically has rods (vertical lines) with beads on them. Each rod represents a different place value.
– For four-digit numbers, you will need four rods:
– Thousands rod
– Hundreds rod
– Tens rod
– Ones rod
2. Assigning Place Values to the Rods
– The rod on the far left represents the Thousands place.
– The next rod to the right represents the Hundreds place.
– The next rod is the Tens place.
– The last rod on the right is the Ones place.
3. Placing Beads to Represent Numbers
– Each bead on a rod represents one unit of that place value.
– To show a number on the abacus, you slide the appropriate number of beads on each rod.
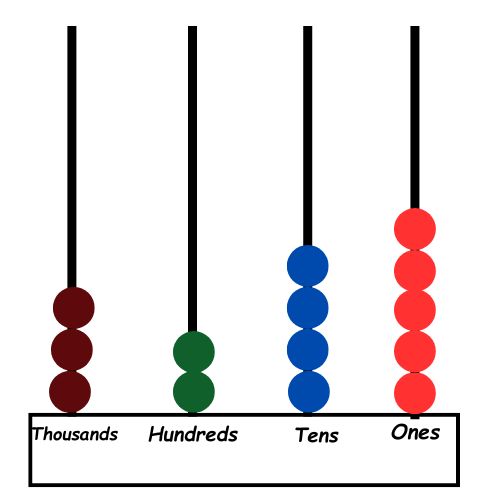
– For example, to represent the number 3,245 on the abacus:
– Thousands rod: Slide 3 beads (represents 3,000).
– Hundreds rod: Slide 2 beads (represents 200).
– Tens rod: Slide 4 beads (represents 40).
– Ones rod: Slide 5 beads (represents 5).
4. Reading the Number on the Abacus
– To read a number from the abacus, you simply count the beads on each rod from left to right.
– Example: If the abacus shows 5 beads on the Thousands rod, 1 bead on the Hundreds rod, 7 beads on the Tens rod, and 3 beads on the Ones rod, the number is 5,173.
5. Practice Examples
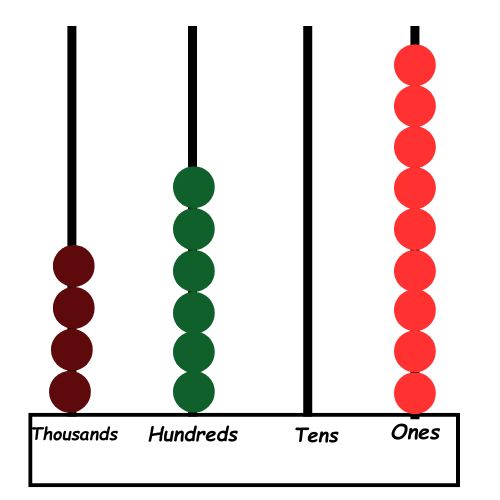
– Example: Show the number 4,609 on the abacus:
– Thousands rod: 4 beads (4,000)
– Hundreds rod: 6 beads (600)
– Tens rod: 0 beads (0)
– Ones rod: 9 beads (9)
6. Changing Numbers on the Abacus
– To change a number on the abacus, move the beads on the appropriate rods.
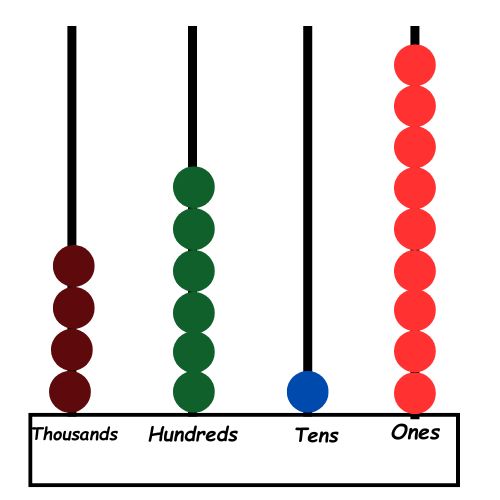
– For instance, if you want to change 4,609 to 4,619:
– Move 1 bead on the Tens rod to add 10.
7. Understanding Place Value with the Abacus
– The abacus helps students clearly see how each digit in a four-digit number has a different value depending on its place.
– For example, the digit 4 in 4,609 represents 4,000, not just 4, because it’s in the Thousands place.
Examples-
3245
4609
4619
Place value, facevalue and expanded form
1. Place Value
– Place value is the value of a digit based on its position in a number.
– For example, in the number 3,582:
– The digit 3 is in the Thousands place, so its place value is 3,000.
– The digit 5 is in the Hundreds place, so its place value is 500.
– The digit 8 is in the Tens place, so its place value is 80.
– The digit 2 is in the Ones place, so its place value is 2.
2. Face Value
– Face value is the actual value of the digit itself, regardless of its place in the number.
– For example, in the number 3,582:
– The face value of 3 is just 3.
– The face value of 5 is just 5.
– The face value of 8 is just 8.
– The face value of 2 is just 2.
3. Expanded Form
– Expanded form breaks down a number to show the value of each digit according to its place value.
– For example, the expanded form of 3,582 is:
– 3,000 + 500 + 80 + 2.
– This shows how the number is made up of each digit’s place value added together.
Summary
– Place value tells us the value of a digit based on its position in the number.
– Face value is the digit itself, regardless of where it is in the number.
– Expanded form shows a number as the sum of each digit’s place value.
This helps students understand the composition of numbers and their values more clearly.
Successor and predecesor
1. Successor
– The successor of a number is the number that comes immediately after it when counting.
– To find the successor, you simply add to the number.
– For example:
– The successor of 5 is 6.
– The successor of 99 is 100.
– The successor of 2,349 is 2,350.
2. Predecessor
– The predecessor of a number is the number that comes immediately before it when counting.
– To find the predecessor, you simply subtract 1 from the number.
– For example:
– The predecessor of 5 is 4.
– The predecessor of 99 is 98.
– The predecessor of 2,349 is 2,348.
Summary
– The successor of a number is the next number in the sequence (add 1).
– The predecessor of a number is the previous number in the sequence (subtract 1).
Skip Counting
Skip counting is a simple math technique where you count forward by numbers other than 1. It’s a way to quickly add or multiply by repeatedly adding the same number. This method is especially useful for understanding multiplication, patterns, and number sequences.
1. Introduction to Skip Counting:
– Start by explaining that skip counting means you “skip” numbers as you count.
– Instead of counting by 1s (like 1, 2, 3, 4, 5…), you count by a specific number, such as 2, 3, 5, or 10.
2. Examples of Skip Counting:
– By 2s: 2, 4, 6, 8, 10, 12…
– By 3s: 3, 6, 9, 12, 15, 18…
– By 5s: 5, 10, 15, 20, 25, 30…
– By 10s: 10, 20, 30, 40, 50, 60…
3. Why It’s Useful:
– Skip counting helps with quicker addition. For example, if you need to add 5 + 5 + 5, you can skip count by 5s to get 15 quickly.
– It’s also the basis for multiplication. If you skip count by 4s and you count 5 times (4, 8, 12, 16, 20), you get 4 × 5 = 20.
Comparision of numbers
When comparing 4-digit numbers, the steps are very similar to comparing smaller numbers, but we pay more attention to the thousands place since it’s the largest digit. Here’s how you can explain it:
1. Understanding the Place Values
– A 4-digit number has four place values: Thousands, Hundreds, Tens, and Ones.
– Example: In the number 5,743:
– 5 is in the thousands place.
– 7 is in the hundreds place.
– 4 is in the tens place.
– 3 is in the ones place.
2. Steps to Compare Two 4-Digit Numbers
– Line Up the Numbers: Make sure the digits are lined up according to their place values.
– Start with the Thousands Place:
– Compare the digits in the thousands place first. The number with the bigger digit here is the bigger number.
– If the digits are the same, move to the next place value (hundreds).
– Compare the Hundreds Place:
– If the thousands digits are the same, compare the digits in the hundreds place.
– Again, the bigger digit means the bigger number.
– Compare the Tens Place:
– If both the thousands and hundreds digits are the same, compare the tens place.
– Compare the Ones Place:
– If all other digits are the same, the digit in the ones place will decide which number is bigger or smaller.
3. Examples of Comparing 4-Digit Numbers
– Example 1: Comparing 4,827 and 4,612
– Look at the thousands place: Both have 4.
– Look at the hundreds place: 8 is greater than 6.
– So, 4,827 > 4,612.
– Example 2: Comparing 3,945 and 3,949
– Look at the thousands place: Both have 3.
– Look at the hundreds place: Both have 9.
– Look at the tens place: Both have 4.
– Look at the ones place: 5 is less than 9.
– So, 3,945 < 3,949.
Odering of numbers
Ordering numbers means arranging them in a sequence, either from smallest to largest (ascending order) or from largest to smallest (descending order). Here’s how to explain it:
1. Ascending Order (Smallest to Largest)
– Definition: When you arrange numbers in ascending order, you start with the smallest number and move to the largest.
– Example: Arrange the numbers 24, 58, 12, and 37 in ascending order:
– Start with the smallest number: 12.
– Then the next smallest: 24.
– Then: 37.
– Finally, the largest number: 58.
– So, in ascending order, the numbers are 12, 24, 37, 58.
2. Descending Order (Largest to Smallest)
– Definition: When you arrange numbers in descending order, you start with the largest number and move to the smallest.
– Example: Arrange the numbers 19, 42, 35, and 7 in descending order:
– Start with the largest number: 42.
– Then the next largest: 35.
– Then: 19.
– Finally, the smallest number: 7.
– So, in descending order, the numbers are 42, 35, 19, 7.
3. Steps to Order Numbers
– Step 1: Look at the first digit of each number (the highest place value).
– For 2-digit numbers, compare the tens place.
– For 3-digit numbers, compare the hundreds place.
– For 4-digit numbers, compare the thousands place.
– Step 2: If the first digits are the same, move to the next place value (tens, hundreds, or ones).
– Step 3: Arrange the numbers based on your comparison.
4. Examples of Ordering Numbers
– Example 1: Ascending Order of 3-Digit Numbers
– Numbers: 345, 567, 234, 456
– Start with the smallest (234) and end with the largest (567).
– Ordered list: 234, 345, 456, 567
– Example 2: Descending Order of 4-Digit Numbers
– Numbers: 2,345; 4,567; 1,234; 3,456
– Start with the largest (4,567) and end with the smallest (1,234).
– Ordered list: 4,567; 3,456; 2,345; 1,234
