Understanding Fraction
Fraction
What is a Fraction?
A fraction is a way to show a part of a whole or a part of a group. It has two parts:
– Numerator (the top number): Tells how many parts we have.
– Denominator (the bottom number): Tells how many parts the whole is divided into.
For example, in the fraction 1/4:
– The numerator is 1, which means we have 1 part.
– The denominator is 4, which means the whole is divided into 4 equal parts.
So, 1/4 means one part out of four equal parts of a whole.
Types of Fractions
There are different types of fractions:
1. Proper Fractions:
– The numerator is smaller than the denominator.
– Example: 2/3 (2 parts out of 3).
2. Improper Fractions:
– The numerator is bigger than or equal to the denominator.
– Example: 5/4 (5 parts out of 4).
3. Mixed Fractions:
– A combination of a whole number and a proper fraction.
– Example: 1 1/2 (One whole and one-half).
How to Read Fractions
Fractions are read as “numerator over denominator.” For example:
– 1/2 is read as “one-half.”
– 3/4 is read as “three-fourths.”
– 5/8 is read as “five-eighths.”
Equivalent fraction
Equivalent fractions are fractions that represent the same part of a whole, even though they may look different. They have different numerators and denominators but are equal in value.
For example:
– 1/2 is equivalent to 2/4 and 4/8.
These fractions look different, but they all represent the same amount (half of something).
How to Find Equivalent Fractions
You can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same number.
1. Multiplying to find Equivalent Fractions
Let’s start with the fraction 1/2:
– Multiply both the numerator and denominator by 2:
1 × 2 = 2
2 × 2 = 4
So, 1/2 = 2/4.
– Multiply both the numerator and denominator by 3:
1 × 3 = 3
2 × 3 = 6
So, 1/2 = 3/6.
2. Dividing to find Equivalent Fractions
Let’s say you have the fraction 6/8:
– Divide both the numerator and denominator by 2:
6 ÷ 2 = 3
8 ÷ 2 = 4
So, 6/8 = 3/4.
Examples of Equivalent Fractions
– 1/3 = 2/6 = 3/9 = 4/12
– 1/4 = 2/8 = 3/12 = 4/16
– 2/5 = 4/10 = 6/15 = 8/20
Fraction on a number line
Fractions on a Number Line
A number line is a straight line with numbers placed at equal intervals along its length. We can use it to show fractions by dividing the space between whole numbers into equal parts.
How to Represent Fractions on a Number Line
1. Draw a Number Line: Draw a horizontal line and mark whole numbers like 0, 1, 2, 3, and so on.
2. Divide the Line into Equal Parts:
– If you want to show 1/2, divide the space between 0 and 1 into 2 equal parts.
– If you want to show 1/3, divide the space between 0 and 1 into 3 equal parts.
3. Mark the Fractions:
– Each part represents a fraction. For example, if you divide the space between 0 and 1 into 4 parts, you get fractions like 1/4, 2/4, 3/4, and finally 4/4, which is equal to 1.
Example: Fractions on a Number Line
1. Representing Fractions like 1/2, 1/4 on a Number Line:
Let’s start with 1/2:
– Draw a number line from 0 to 1.
– Divide the space between 0 and 1 into 2 equal parts.
– The first part will be 1/2, and the second part is 2/2 (which is equal to 1).
Now let’s place 1/4:
– Divide the space between 0 and 1 into 4 equal parts.
– The points will be 1/4, 2/4 (which is 1/2), 3/4, and 4/4 (which is 1).
So, the number line would look like this:
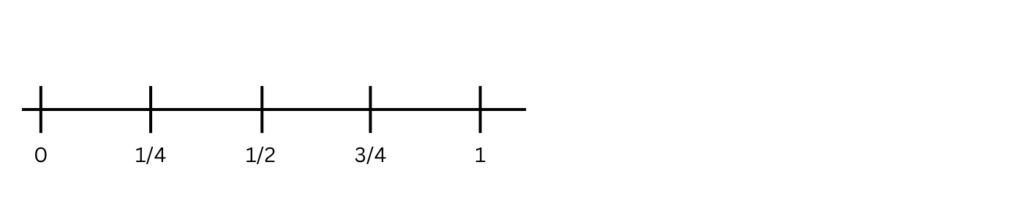
2. Representing Mixed Fractions like 1 1/2 on a Number Line:
Mixed fractions have a whole number and a fraction. Let’s represent 1 1/2 on a number line:
– Start by marking whole numbers 0, 1, 2, 3 on the number line.
– Between 1 and 2, divide the space into 2 equal parts to show the fraction 1/2.
– 1 1/2 will be halfway between 1 and 2.
The number line will look like this:

Important Tips for Fractions on a Number Line:
1. Proper Fractions: Always lie between 0 and 1 (Example: 1/2, 3/4).
2. Improper Fractions: Are greater than 1 and lie beyond 1 on the number line (Example: 5/4, 7/3).
3. Mixed Fractions: Are shown by moving beyond whole numbers (Example: 1 1/4, 2 1/2).
Simplest form of fraction
The simplest form of a fraction (also called the lowest terms) is when the numerator and the denominator cannot be divided by any common factor except 1. In other words, it’s when the fraction is reduced as much as possible.
For example:
– The fraction 4/8 can be simplified to 1/2.
– The fraction 6/9 can be simplified to 2/3.
How to Simplify a Fraction
To simplify a fraction, follow these steps:
1. Find the Greatest Common Factor (GCF):
– The GCF is the largest number that can divide both the numerator and the denominator.
2. Divide Both Numerator and Denominator by the GCF:
– Divide both the top number (numerator) and the bottom number (denominator) by the GCF.
Example 1: Simplify 12/16
1. Find the GCF of 12 and 16.
– The factors of 12 are: 1, 2, 3, 4, 6, 12.
– The factors of 16 are: 1, 2, 4, 8, 16.
– The GCF is 4 (the largest number that divides both 12 and 16).
2. Divide both the numerator and the denominator by 4:
– 12 ÷ 4 = 3
– 16 ÷ 4 = 4
So, 12/16 simplified is 3/4.
Example 2: Simplify 9/12
1. Find the GCF of 9 and 12.
– The factors of 9 are: 1, 3, 9.
– The factors of 12 are: 1, 2, 3, 4, 6, 12.
– The GCF is 3.
2. Divide both the numerator and the denominator by 3:
– 9 ÷ 3 = 3
– 12 ÷ 3 = 4
So, 9/12 simplified is 3/4.
Conversion of improper and mixed fraction
1. Improper Fractions:
An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number).
– Example: 7/4, 9/5, 12/3
In each of these examples, the numerator is bigger than the denominator.
2. Mixed Fractions:
A mixed fraction (also called a mixed number) is made up of two parts:
– A whole number
– A proper fraction (where the numerator is smaller than the denominator).
– Example: 2 3/4, 1 1/5, 3 2/3
Here, the fraction shows the extra part beyond the whole number.
How to Convert Between Improper and Mixed Fractions
To convert an improper fraction into a mixed fraction:
– Step 1: Divide the numerator by the denominator.
– Step 2: The quotient (result of division) will be the whole number part of the mixed fraction.
– Step 3: The remainder will be the numerator of the proper fraction, and the denominator stays the same.
Example: Convert 7/4 to a mixed fraction:
1. Divide 7 ÷ 4 = 1 remainder 3.
2. The quotient is 1 (this is the whole number part).
3. The remainder is 3, so the new fraction is 3/4.
So, 7/4 = 1 3/4.
2. Converting Mixed Fractions to Improper Fractions**
To convert a mixed fraction to an improper fraction:
– Step 1: Multiply the whole number by the denominator.
– Step 2: Add the result to the numerator.
– Step 3: The sum will be the new numerator, and the denominator stays the same.
Example: Convert 2 3/5 to an improper fraction:
1. Multiply the whole number 2 x 5 = 10 .
2. Add the numerator 10 + 3 = 13 .
3. The new fraction is 13/5.
So, 2 3/5 = 13/5.
Comparision and ordering of fraction
1. Comparing Fractions with the Same Denominator
If two fractions have the same denominator, the fraction with the larger numerator is the bigger fraction. For example:
– Compare frac 3/8 and frac 5/8:
Since the denominators are the same, we just compare the numerators: 3 and 5.
– Answer: frac5/8 is greater than frac3/8.
2. Comparing Fractions with Different Denominators
When the denominators are different, we need to make the denominators the same by finding a common denominator.
Steps:
– Find the least common denominator (LCD) of the two fractions.
– Convert both fractions to equivalent fractions with the same denominator.
– Compare the numerators.
Example: Compare frac 1/4 and frac 1/3.
– The least common denominator of 4 and 3 is 12.
– Convert 1/4 to 3/12 and 1/3 to 4/12.
– Now compare 3/12and 4/12:
– **Answer:1/3is greater than 1/4.
3. Ordering Fractions
To order fractions from least to greatest or greatest to least, follow these steps:
– Find a common denominator for all the fractions.
– Convert each fraction to an equivalent fraction with the common denominator.
– Compare the numerators to order the fractions.
Example: Order 1/2, 1/4, 3/4 from least to greatest.
– The least common denominator is 4.
– Convert:
– 1/2 = 2/4
– 1/4 = 1/4 (already in the correct form)
– 3/4 = 3/4
– Now compare: 1/4, 2/4, 3/4.
– Answer: 1/4, 1/2, 3/4.
Addition and subtraction of fraction
1. Adding and Subtracting Fractions with the Same Denominator
When the denominators (bottom numbers) are the same, we simply add or subtract the numerators (top numbers) and keep the denominator the same.
Addition Example:
Add 3/8+ 2/8:
– The denominators are the same (8), so we add the numerators:
3 + 2 = 5 .
– Keep the denominator:
5/8.
Answer:3/8 + 2/8 = 5/8.
Subtraction Example:
Subtract 5/9 – 2/9:
– The denominators are the same (9), so we subtract the numerators:
5 – 2 = 3 .
– Keep the denominator:
3/9.
Answer: 5/9 – 2/9 = 3/9, which simplifies to 1/3.
2. Adding and Subtracting Fractions with Different Denominators
When the denominators are different, we need to follow these steps:
– Step 1: Find the least common denominator (LCD) of the fractions.
– Step 2: Convert both fractions to equivalent fractions with the same denominator.
– Step 3: Add or subtract the numerators and keep the denominator the same.
Addition Example:
Add 1/4 + 1/6:
– Step 1: Find the least common denominator of 4 and 6. The LCD is 12.
– Step 2: Convert the fractions to have the same denominator:
– 1/4 = 3/12 and frac1/6 = 2/12 .
– Step 3:Now, add the numerators:
3 + 2 = 5 .
Answer:1/4 + 1/6 = 5/12.
Subtraction Example:
Subtract 3/5 – 1/3:
– Step 1: Find the least common denominator of 5 and 3. The LCD is 15.
– **Step 2:** Convert the fractions to have the same denominator:
– 3/5 = 9/15 and 1/3 = 5/15 .
– Step 3:Now, subtract the numerators:
9 – 5 = 4 .
Answer: 3/5 – 1/3 = 4/15.
3. Adding and Subtracting Mixed Numbers
A mixed number consists of a whole number and a fraction. To add or subtract mixed numbers, follow these steps:
Steps:
1. Add or subtract the whole numbers separately.
2. Add or subtract the fractions separately (convert to a common denominator if needed).
3. Combine the whole number and fraction parts.
Addition Example:
Add 2 1/4 + 1 2/3 :
– Add the whole numbers: 2 + 1 = 3 .
– Add the fractions:
– 1/4 and 2/3 have different denominators, so find the LCD (12).
– 1/4 = 3/12 and 2/3 = 8/12.
– Add: 3/12 + 8/12 = 11/12.
– Combine the whole number and the fraction:
3 11/12.
Answer:*2 1/4 + 1 2/3 = 3 11/12.
Subtraction Example:
Subtract 3 5/6 – 1 1/4:
– Subtract the whole numbers: 3 – 1 = 2 .
– Subtract the fractions:
– 5/6 and 1/4 have different denominators, so find the LCD (12).
– 5/6 = 10/12 and 1/4 = 3/12.
– Subtract: 10/12 – 3/12 = 7/12.
– Combine the whole number and the fraction:
2 7/12.
Answer: 3 5/6 – 1 1/4 = 2 7/12.
